| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
Tags
- JAVA 재귀함수
- root passwd
- 리눅스 사용권한
- 코드스테이츠
- O(log n)
- AOP
- Java
- Spring
- 스키마 설계
- 스키마 디자인
- git 설정
- ubuntu passwd
- char to int
- Spring MVC
- custom exception
- 함수형 인터페이스
- mapstruct
- git workflow
- ubuntu
- RestControllerAdvice
- 자료구조
- Spring 예외처리
- 탐욕 알고리즘
- http 응답코드
- ubuntu 패스워드
- file i/o
- REST HTTP API
- 배열 탐색
- N:N
- set-version
Archives
- Today
- Total
개발소설
[알고리즘] 시간복잡도 개념 본문
시간복잡도
- 문제를 해결하기 위한 알고리즘의 로직을 코드로 구현 할때 입력값의 변화에 따라 연산을 실행시 연산 횟수에 비해 시간이 얼마나 걸리는가를 고려하는것
- 효율적인 알고리즘을 구현하는것은 입력값이 커짐에 따라 증가하는 시간의 비율을 최소화 하는것
Big-O 표기법
- 시간 복잡도의 표현법에는 Big-O(빅-오), Big-Ω(빅-오메가), Big-θ(빅-세타)가 있다.
- 시간 복잡도를 각각 최악, 최선, 중간(평균)의 경우에 나타내는 방법이다.
- 그중 최악의 경우를 나타내는 Big-O 표기법을 많이 사용 하는데 프로그램이 실행하되는 과정에서 소요되는 최악의 시간까지 고려하기 때문이다.
- 최선의 경우나 평균의 경우로 문제가 해결 되면 좋겠지만 그렇지 않은 경우에 대하여 대처 할 수 있다.
O(1)
- 입력값이 아무리 커져도 즉시 해결 할 수 있는 경우
- 배열의 인덱스 값을 입력받아 바로 배열의 인덱스로 접근하여 값을 리턴하는 경우
int check(int i){
return arr[i];
}
O(n)
- 입력값이 증가함에 따라 시간이 같은 비율로 증가하는것 - 입력값에 따라 일정하게 증가한다.
- 입력값이 1일때 1초가 걸리고, 입력값이 100일때 100초가 걸리는 경우
- 입력값에 따라 반복문을 N의 크기만큼 도는것 - for문
void time(int n){
for(int i=0; i<n i++){
result++;
}
return result;
}
O(log n)
- 경우의 수를 절반으로 줄여가며 시간을 줄이는 방법
- 주로 이진트리 탐색
- Up & Down 게임과 비슷하다.
- 1~100 사이의 수를 찾는다. (35)
- 절반인 50을 먼저 찾았을때 50보다 크면 up 작으면 down
- down 이므로 50의 절반인 25 찾기
- 이런식으로 경우의 수를 절반으로 줄여가며 해당 값을 찾는다.

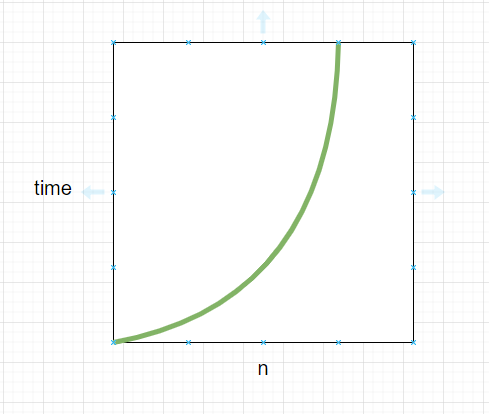
O(n^2)
- 입력값에 따라 시간이 제곱의 비율로 증가하는것
- 입력값이 1일떄는 1이지만, 2일때는 4, 5일때는 25, 이처럼 시간이 기하급수적으로 증가하는것
- 주로 2중 for문
void time(int n){
for(int i=0; i<n; i++){
for(int j=0; j<n; j++){
result++;
}
}
return result;
}
O(2^n)
- 가장 느린 시간 복잡도로 시간이 아주 오래 걸리는 경우
- 구현하는 알고리즘이 해당 시간복잡도를 가진다면 다른 방법을 사용하는게 좋다.
- 피보나치 수열이 해당 시간 복잡도를 가진다.
- A4 용지를를 42번 접으면 지구에서 달까지의 거리보다 더 길다고한ㄷ....
public int fibonacci(int n) {
if(n == 1) return 1;
if(n == 2) return 1;
return fibonacci(n - 1) + fibonacci (n - 2);
}
'CS > 알고리즘' 카테고리의 다른 글
| [알고리즘] 순열(permutation), 조합(Combination), 중복순열 (0) | 2023.03.23 |
|---|---|
| [알고리즘] 탐욕(Greedy) 알고리즘 (0) | 2023.03.22 |
| [JAVA] 재귀함수(Recursion) (1) | 2023.03.14 |
| JAVA 배열에서 새로운 요소를 추가하기 (0) | 2023.03.03 |
| 피보나치 수열 - 배열 (0) | 2023.02.23 |
Comments

